CRDTs in a Nutshell

CRDT: Conflict-Free Replicated Data Type

CRDTs are shared data structures with superpowers. They enable independent modification and still stay in sync. It means that if two users, Alice and Bob, decide to change a key in a CRDT-based hash map, they don't need to coordinate beforehand. Alice can change the value of key "foo" to 1, while Bob can make it 3. Eventually, when Alice and Bob sync, it is guaranteed that neither of their changes will be lost. Moreover, the shared data structure will not be corrupted. It will eventually converge to a single value that Alice and Bob agree on.

This post will look at the theoretical underpinning of CRDTs. We will implement two different CRDTs: GCounter (or Grow only counter) and LWW set (Last Writer Wins set). We will also analyze their applications, compare them with the main alternative: Operational Transformations and understand their limitations.

CRDTs Theory

Thanks to order theory, CRDTs are robust to data corruption amid concurrent edits and converge to a canonical value over time. There are a few concepts at work here. First is the notion of order. Second is the concept of a join or merge. The third is semilattice.

Order

An order is a binary relation. For example, we can say, in the set of integers 2 < 3. The less than operator here is the order. An order could be total or partial. A less than operator is a total order over a set of integers.

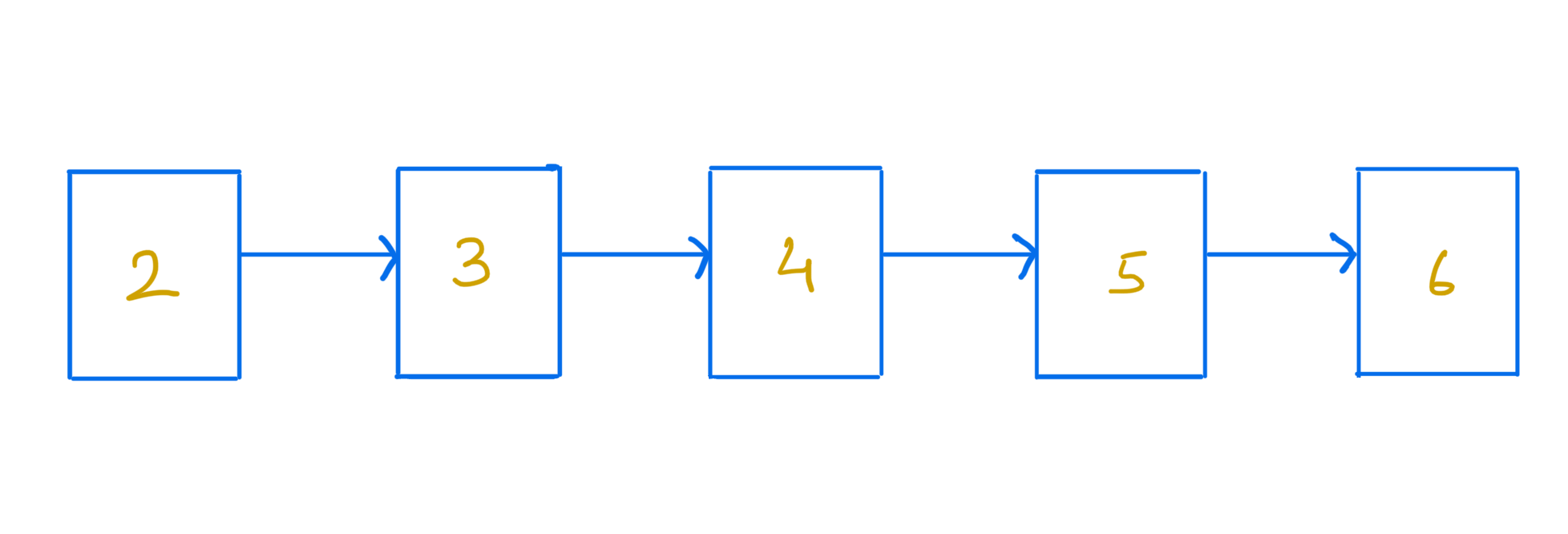A totally ordered set of integers

An example of a partial order is the "located-in" relation. Consider a set {USA, NYC, Germany, Berlin}. NYC is located in USA, and Berlin in Germany. We cannot compare USA and Germany with the located-in operator. Neither USA is located in Germany, nor Germany is located in the USA.

In an ordered set, an upper bound is an element greater than or equal to any other element. The join or merge operation on two elements is the least upper bound in such a set.

For example, in a set of integers, the join of 2 and 5 will be 5. There's no integer smaller than 5 that's an upper bound on both 2 and 5. 7 is an upper bound on 2 and 5, but it's not the least upper bound since 5≤7.

Recall that the less than and equal operator is a total order for a set of integers. A curious property of total order is that joining two elements will result in one of the two elements. It is because every element can be directly compared to every other element.

It is not valid for a partial order. Let's extend our set of locations from above: {North America, USA, NYC, SF, Europe, Germany, Berlin, Munich} Here, the join operation on "NYC" and "SF" cannot produce either "NYC" or "SF" because the two are incomparable. The "USA" and "North America" are the upper bounds for "NYC" and "SF". "USA" is the least upper bound. It means that the join operation on "SF" and "NYC" results in "USA".

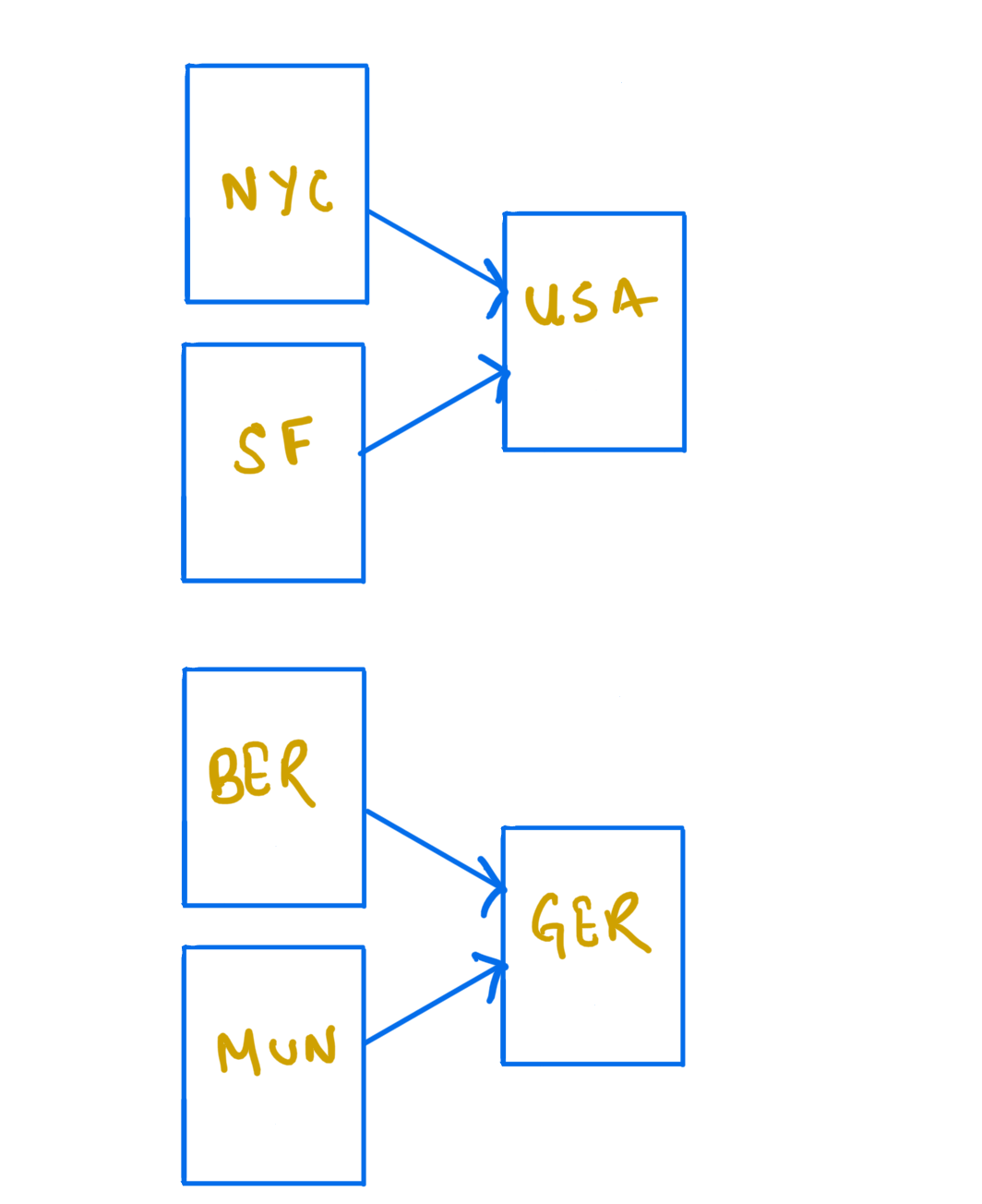A partially ordered set of locations

Join

The join or merge operation in our pre-defined set with an order must follow the three algebraic rules. It should be commutative, associative, and idempotent.

Commutativity means it doesn't matter in which order we join two elements. It is similar to how it doesn't matter in which order we add or multiply two integers.

Associativity means if we want to join three elements, we can pick any two at a time and then join the result with the remaining element.

Idempotence means that we can join an element with itself any number of times, and we will still end up with the same element.

Semilattice

A set with an order is a join semilattice if we can take any two elements from the set and find a join for them. It is easier to see it in the case of the total order, for example, the set of integers and the less than and equals operator. For any two elements, the least upper bound will be one or the other of those two integers.

It is not straightforward for the partial order. Again, consider our set of locations. We cannot perform a join on "USA" and "Germany" because there is no upper bound. Both of these countries are incomparable. This set and the corresponding located-in order don't form a join semilattice. However, if we add "Earth" to this set, it will become a join-semilattice.

Here is another example of the difference between total order and partial order. It is more abstract but more familiar. A binary search tree is totally ordered, whereas a binary heap is partially ordered. In a binary search tree, every parent node must be bigger than its left child and smaller than the right child. This property is responsible for the total order in this data structure. In a max heap, every parent element must be bigger than both of its children. However, the children remain relatively unordered. Both data structures are ubiquitous, but each has a different purpose. A binary search tree can quickly find an element. The time it takes is proportional to the logarithm of the number of elements in the tree. On the other hand, a heap is instrumental in quickly finding the extreme (min or max) elements in constant time.

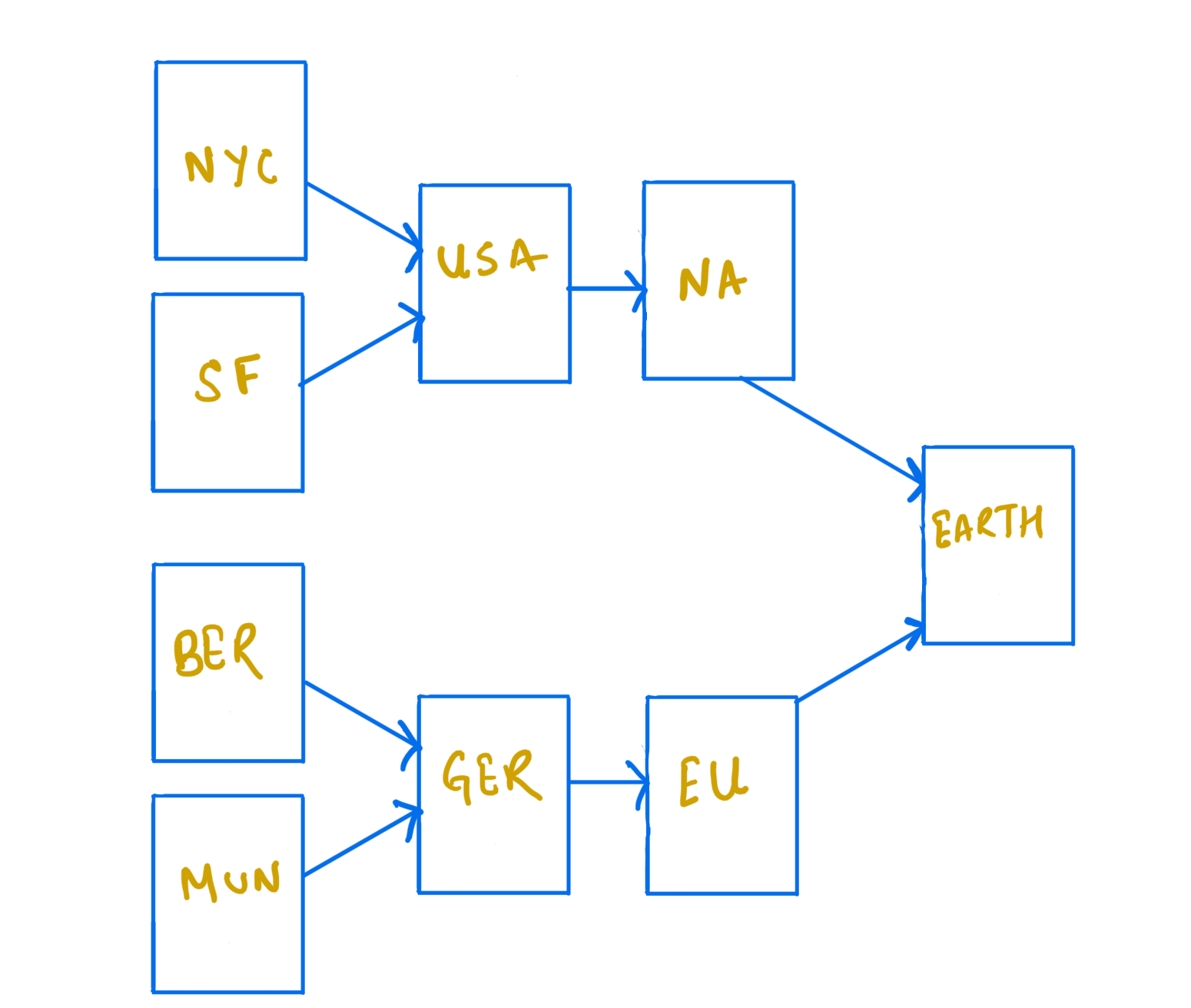A partially ordered set of locations

According to Wikipedia, state-based CRDTs:

send their full local state to other replicas, where the states are merged by a function which must be commutative, associative, and idempotent. The merge function provides a join for any pair of replica states, so the set of all states forms a semilattice. The update function must monotonically increase the internal state according to the same partial order rules as the semilattice.

It raises a question. How CRDTs deal with a partial order? How can two replicas be merged that cannot be compared? This is, in fact, the most intriguing case when concurrent modification leads to conflicts.

This scenario is analogous to "merge conflicts" in git. When two developers modify the same line of code in different commits, there is a conflict when they merge their code. Generally, developers resolve conflicts offline following a specification.

Similarly, concurrent edits create a conflict in a CRDT. For example, if Alice and Bob are writing a letter to Charlie. They might start at the same time. Alice might type the first line as "Hi Charlie". Bob, in his editor, may type it as "Hello Charlie". In this case, the CRDT-based text editing software won't be able to automatically converge on a value. In such cases, the end-user has to intervene. Alternatively, applications may use a heuristic. For example, the editor can produce the first line as "HiHello Charlie". Later, either Bob or Alice can fix the word "HiHello" to something sensible.

The values in CRDTs increase monotonically according to some order. CRDTs diverge until they eventually converge. Having briefly looked at order theory, we can see that CRDTs converge mathematically towards the least upper bound of all possible values.

Intuitively we can see that the state is merging. As the nodes sync, they update their local value based on the value they see in the received message. The final shared state is equivalent to the result of some correct sequential execution.

The most fascinating bit is that CRDTs converge to a consensus value without using any consensus algorithm like Raft, Paxos, PBFT, etc. It means that any new state update can execute immediately. Network latency or faults won't slow down the system.

Types of CRDTs

There are two types of CRDTs: state-based and operation based. Both are theoretically equivalent. However, when it comes to implementation, they offer different trade-offs.

The state-based CRDTs are easier to implement. They do not require any guarantees from the underlying network. The problem is that they are generally inefficient. The entire state of every replica is eventually transmitted over the network.

The operation-based CRDTs only transmit the update operation and hence consume less bandwidth. However, such CRDTs require a reliable underlying network. The operations must be kept from being dropped or duplicated and delivered in a causal order.

CRDT Examples

Some examples of CRDTs are: G counter, PN counter, G set, 2 Phase set, Last Writer Wins set, OR set, etc. For collaborative text editing use cases, generally, sequential CRDTs are used as described in RGA and WOOT, etc. Below are simple implementations of a G counter and an LWW set.

G counter

A grow-only counter is the simplest CRDT. It can only increase in one direction. A use case for such a data structure could be to track the number of "plays" for a video or a song.

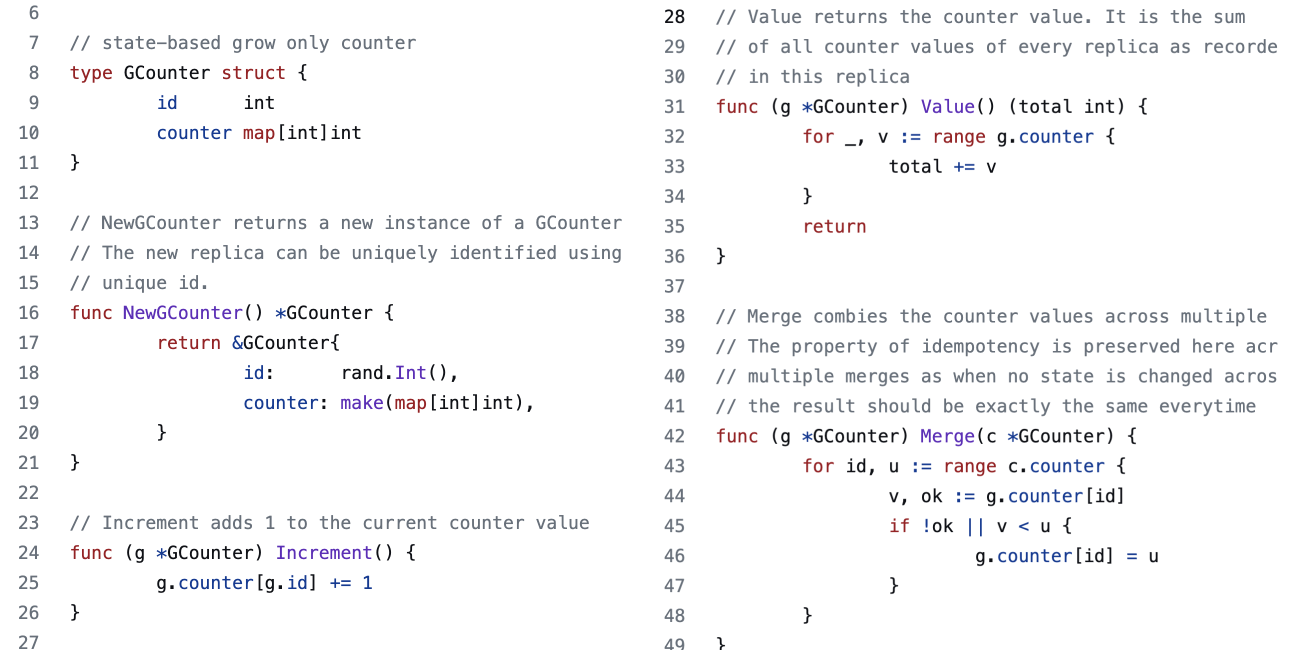A Gcounter implementation in Go

The counter is implemented as an integer-to-integer hash map. The map has an entry for every other replica that this copy knows about. When an actor hears from another, it merges their value into the counter using the merge function.

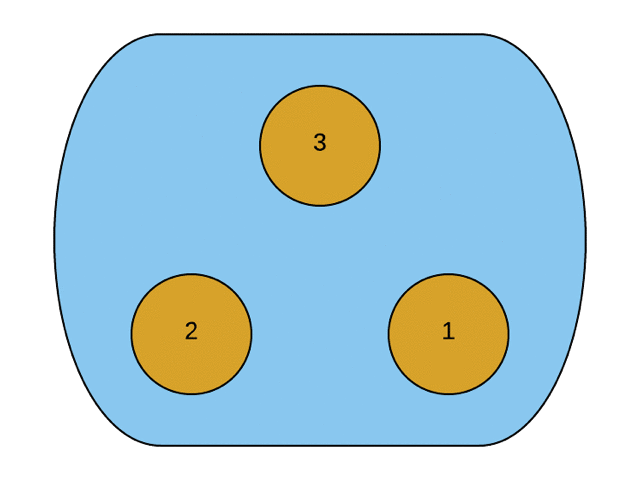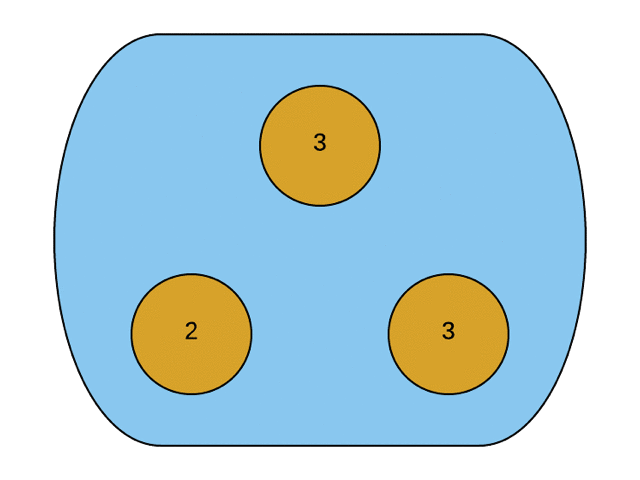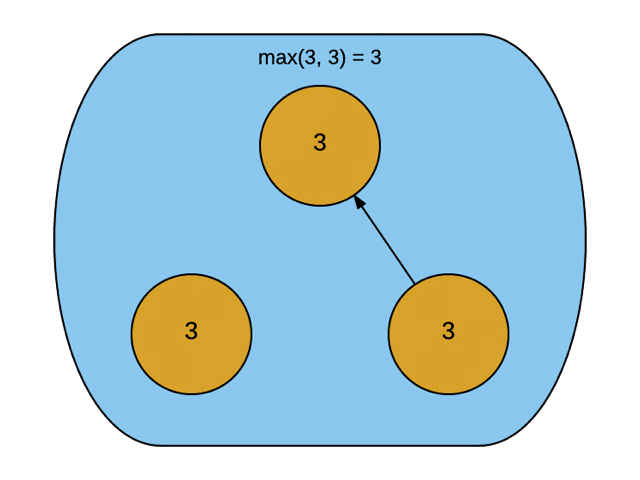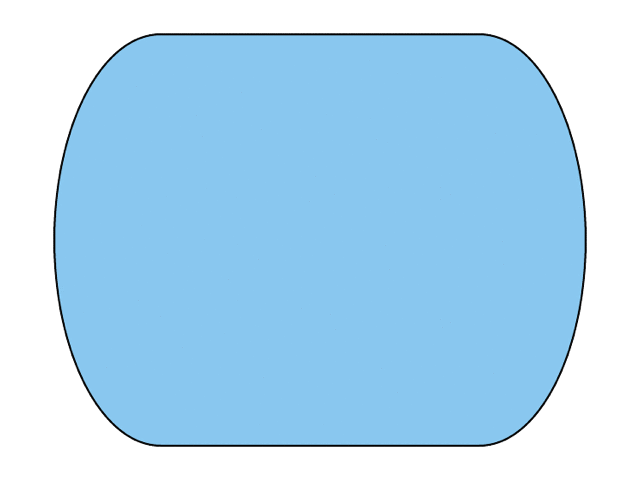
The Merge function iterates through the received counter and updates the keys if it is not present in the current replica or its value is lower than the received value. The maximum observed value is chosen because that is the least upper bound on a set of integers.

The Value function returns the current value of the counter. The point to note here is that the system's value is the sum of all observed counters. It makes sense. Ideally, the value should be the total number of increment operations that all the replicas in the system have seen in aggregate.

source: http://jtfmumm.com/blog/2015/11/24/crdt-primer-2-convergent-crdts/

One might find it more intuitive to implement a counter as an integer instead of a hash map, but that design has a flaw. Imagine this scenario. A system has 3 replicas of a counter with values 3, 2, and 1. It means that the system, in total, has seen 6 increments. When node 1 syncs with node 2, both will update their counters to the maximum of each other's value. Their new shared value will become 3. When node 3 syncs with the other two, it will update its counter value to 3. This is a problem. We are expecting the counter to be 6, not 3.

LWW set

Let's look at another CRDT, the Last Writer Wins Set. The semantics is as the name suggests. The set allows you to add or remove any item.

Under the hood, such as set maintains two different sets. One for additions and the other for removals (called the tombstone set). An item is a member when the following two conditions hold. One, it is in the "add" set. Second, it is not in the remove set or was added in the remove set before it was added in the "add" set.

LWW set implementation in Go

Such a set can have an "add" or a "remove" bias. When the timestamps are equal, bias resolves the conflict. Note that a timestamp collision is likely to happen after two replicas merge.

Operational Transform

CRDTs offer an approach for achieving eventual consistency in distributed systems. They are designed to handle conflicts between concurrent updates to the same data, ensuring that all replicas eventually reach the same state. It makes CRDTs a handly tool to implement collaborative software such as text editors. However, it is crucial to note that the current state of the art collaborative editors, such as Google Docs, does not use CRDTs. Instead, it uses Operational Transform algorithms. Both Operational Transform and CRDTs-based algorithms strive to converge independent data modifications.

The Operational Transform algorithm, in a nutshell, works by sending the indices at which the edit was made to other nodes. The received index must be transformed if the local copy has that index occupied. Index transformations happen in a central server. The server keeps the authoritative copy of the data that users are working on.

Operation Transforms are battle tested. However, they are less flexible when it comes to network architecture. It relies on a centralized server for sequencing edits to prevent unexpected data races. CRDTs don't share this limitation because they are a local data structure. Software built on CRDTs can talk to other instances over a p2p connection. No coordination is required.

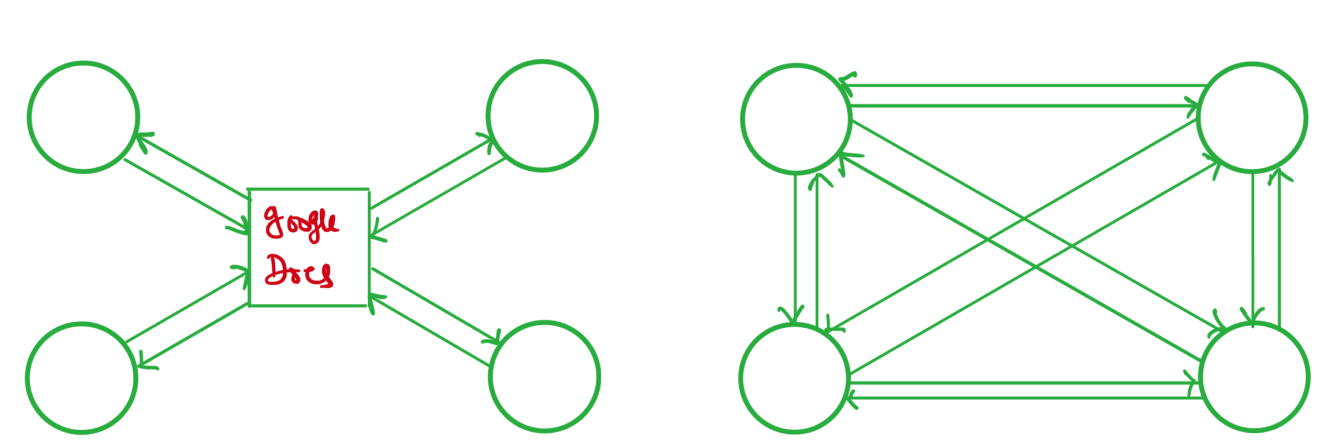OT vs CRDT network topology

The central Operational Transform server can become a performance bottleneck when a large number of users use it at the same time. On the other hand, writing p2p applications may be challenging. Also, notice that p2p networking is not required to use CRDTs. It works as well in a client-server architecture.

CRDT Limitations

CRDTs guarantee convergence, but not without cost. One of the main issues with CRDTs is that they could get memory hungry. Based on the examples discussed above, one might have spotted a pattern. These data structures only accrete. For example, a GSet keeps adding new elements without ever deleting anything. A Two-Phase set uses a tombstone set to record retractions.

CRDTs need to store the history of all edits. Garbage collection is not trivial. It is impossible to know when a disconnected node might come back online and wants to merge all the changes to arrive at the current system state.

There are some heuristics for garbage collection, but only with trade-offs. For instance, such GC techniques might require synchronization, which hurts performance. It is hard to implement CRDTs-based algorithms in resource-constrained environments such as edge computers, IoT devices, etc.

In Closing

In this post, we explored Conflict-Free Replicated Data Types (CRDTs), shared data structures that enable independent modifications while remaining in sync. Using order theory concepts, CRDTs ensure convergence to a single value over time without using consensus protocols. We also looked at some simple CRDT implementations, such as GCounter and LWW set, and discussed their applications and limitations. CRDTs offer flexibility in network architecture but can be memory-intensive since they store edit histories.