A Few Notes on Probability Theory

Textbook examples in probability theory books tend to deal with artificial problems like tossing a coin or throwing a die. In toy experiments like these, one outcome is entirely independent of the other. In such cases, it is relatively easy to analyze the probabilities of individual events. For example, it is easy to see that a fair coin turns up heads half of the times on average.

Let's take the example of two coin tosses. Let's label the event of getting heads in the first toss as A and second as B. Then the probability of A and B happening together is defined to be the intersection of A and B:

$$A \cap B$$

This can be visualized using a Venn diagram:

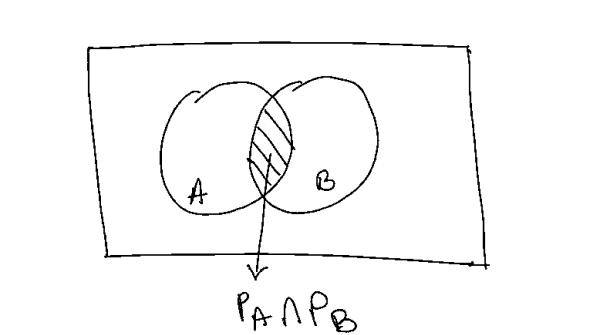
Now we reason that since the first coin toss does not impact the second coin toss in any way so the intersection of two probabilities must be the same as their product:

$$P_A \times P_B$$

In this case, the probability of getting two heads in a row will be:

$${1 \over 2} \times {1 \over 2} = {1 \over 4} $$

So that means:

$$ P_A \cap P_B = P_A \times P_B $$

But this result does not always hold. In fact, it rarely holds outside of trivial textbook examples.

CONDITIONAL PROBABILITY

Imagine you want to analyze the probability for it to rain today, and you already know that it rained yesterday. Intuitively you know that raining a day before makes it more likely to rain on the present day.

It is a conditional analysis. Conditional probability is defined as the probability of event A happening given that event B has already happened. If A and B are two coin tosses as described earlier, then what is the probability of the second coin landing heads if the first has already landed heads? It is straightforward. We know one toss doesn't affect the other, so it is the same:

$$ P_{B|A} = P_B$$

But in the case of the rain, as we saw before, raining a day earlier makes it more likely to rain on the present day. That means:

$$ P_{A|B} > P_B$$

In such a case of dependence, conditional probability is defined as the ratio of the probability of observing both A and B to the probability of observing event B (independent of A).

$$ P_{A|B} = \frac{P_A \cap P_B}{P_B}$$

Represented in the Venn diagram as:

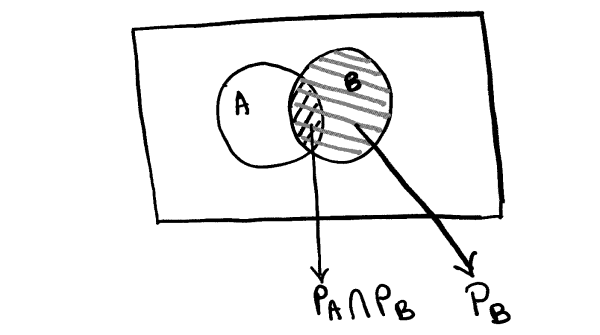
BAYES THEOREM

From set theory, we understand that set intersection is commutative. That is:

$$ A \cap B = B \cap A $$

In this context, it implies:

$$ P_{A|B} \times P_B = P_{B|A} \times P_A $$

This result looks very close to a fundamental theorem of high applicability. Bayes theorem is abstract and counterintuitive. I always found it difficult to grasp it fully. Let alone applying it in real problems. But it can be constructed relatively easily using simple equations as we saw above.